From PDEs to Hines' solver

To understand and model electrical activity in neurons and neural networks, it is necessary to solve equations on current flows. When we take a single neuron into account, we should distribute that current flow over time and space which takes us to solve a PDE (Partial differential equation) instead of a more simple ODE. Such a cable equation allowing spatial variation looks like this:

In order to simplify this equation, we discretize over space by dividing our model to compartments, then apply the conservation of charge to determine the current flow of these interconnected compartments. For time discretization if we choose the trapezoidal rule, the so called Crank-Nicolson method is used. Crank-Nicolson is an implicit method thus it's stable for any choose of Δt. Furthermore this method has a numerical accuracy of O((Δt)²) unlike the backward and forward Euler methods O(Δt) accuracy.

Now considering linear cables, the coefficients of the system can be arranged in a tridiagonal, while a system of multiple branches can be arranged in an also symmetric (to the diagonal) matrix. The latter kind of arrangement is done with Hines numbering. This recursive decreasing enumeration of grid points is accomplished as follows:

1. Choose a branch, that is only connected at one end = 'trunk' - denote it with the highest number
2. Starting from the 'trunk' do a breadth-first or a depth-first searchⁱ towards the other branches while numbering them decreasingly

This enumeration yields a Hines matrix - H - satisfying three conditions: (1) the diagonal elements are nonzero; (2) H_ij is nonzero only if H_ji is nonzero; and (3) H has up to one nonzero element right to the diagonal in any row - and thus no more than one nonzero element below the diagonal in any column.

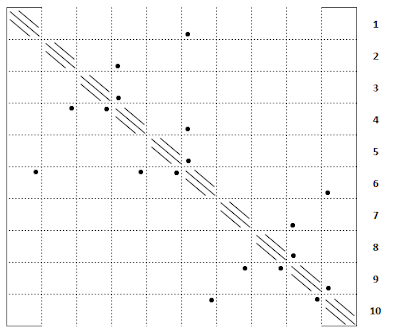
Here's an example of a branched neuronal structure and Hines numbering using depth-first search:

And the corresponding Hines matrix:

Gaussian elimination now can be applied directly (without pivoting) to get the solution of the membrane voltage vector at the next time step. Concretely if H is the Hines matrix then equation solving for V^t+1 is HV^t+1 = V^t by putting the [H | V^t] matrix into the form of [I | h] using Gaussian elimination, where I is the identity matrix. Here h = V^t+1 = H^-1V^t.

In MOOSE, Hines' solver has the main advantage to optimize the calculation of coupled neuronal compartments quite efficiently. On the other hand, this method only can be utilized when the coupled equations describe a branching tree-like structure without closed loops. Thus it is not an option for applying to e.g. gap junctions or a whole network of cells that has loops in them.

ⁱ A more general algorithm can be described as: "Sequentially number nodes that have at most one unnumbered neighbor until there are no unnumbered nodes left." - Christof Koch

Sources

• The Book of Genesis
• Biophysics of Computation: Information Processing in Single Neurons - Christof Koch
• Numerical Methods for Neuronal Modeling - Michael V. Mascagni
• Efficient Computation of Branched Nerve Equations - Michael Hines
• Tutorial: Simulations with Genesis using hsolve - Hugo Cornelis