This post is about methods for solving ODEs (Ordinary Differential Equations) and about such methods used particularly in GENESIS, the ancestor of MOOSE (Multiscale Object-Oriented Simulation Environment), for neuronal modeling.
Before we discuss the methods themselves, there's a need for mentioning stiffness. We consider an ODE stiff if it has abrupt transitions in it, like an action potential. Basically stiffness measures the difficulty of solving an ODE numerically.
Stiff systems
Then we can distinguish two kinds of methods for ODEs: explicit and implicit. A non-stiff ODE can be solved by an explicit method, which is rather simple to implement / use. While a stiff ODE requires an implicit method as explicit ones tend to loose stability, which results in over- or undershooting, when solving such ODEs. On the other hand, implicit methods are more complicated and thus less trivial to implement.
Methods can be also classified by how the accuracy depends on the integration step size (Δt). For example, O((Δt)2) means that the difference between the exact and actual solution increases quadratically as we increase Δt.
Explicit methods
Forward Euler
The Forward Euler method is the most simple but less accurate of the methods discussed here. It's comprehensible then that it's rarely used in GENESIS and MOOSE.
Exponential Euler
This exponential integrator method is accurate for neural models with active channels and few compartments. It assumes the following:
The solution can be approximated as:
where
Although exponential Euler is an explicit method it is not affected by stiffness. GENESIS and MOOSE both have implementation of the method.
Adams-Bashforth
It uses past values of f(t) to approximate higher derivatives, thus it's computationally more efficient than the previous methods, but it's more sensitive to truncation errors as the repeated use of preceding values leads to cumulative errors of large amount. It is advised to use when f(t) varies barely or smoothly. Adams-Bashforth is also present in GENESIS and MOOSE.
Implicit methods
Backward Euler
As Backward Euler method is implicit it remains stable solving stiff ODEs no matter how large is Δt (though a larger Δt can still mean larger truncation error). This differs from the Forward Euler in that the function f is evaluated at the end point of the step, instead of the starting point. Backward Euler is implemented in both GENESIS and MOOSE.
Heun method
It is also called as Crank-Nicholson or second order Runge-Kutta method. It's based upon the trapezoidal rule of numerical integration. It calculates the derivative both at the starting and the end point then take their average. Basically it makes use of the forward and backward Euler method. Solving stiff ODEs with large step size, it approaches instability resulting in damped oscillations, under- and overshooting (due to forward Euler being "part of it"). It is advised to apply for high precision calculations with small Δt.
Heun method
Conclusion
When we choose a method to simulate a neuronal model or to solve any ODE first we should consider the stiffness of the ODE and choose an explicit or implicit method accordingly. Then we should take into account the "big Oh" of accuracy dependence on step size of the method and set Δt likely. Testing of Δt with different values is advised: if increasing Δt evokes no change in the results, it can be further increased; if decreasing Δt evokes changes it should be further decreased, though one may keep in mind that too small step size can result in round-off errors.
I am going to write my next post on Hines' solver and about the progress of NNGPU, the CUDA powered trainable neural network.
Sources
- Book of Genesis
- Numerical Methods for Neuronal Modeling - Michael V. Mascagni
- Numerical Methods for Ordinary Differential Equations - Didier Gonze



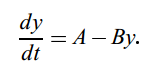






No comments:
Post a Comment